Ce qu'on peut faire avec Excel

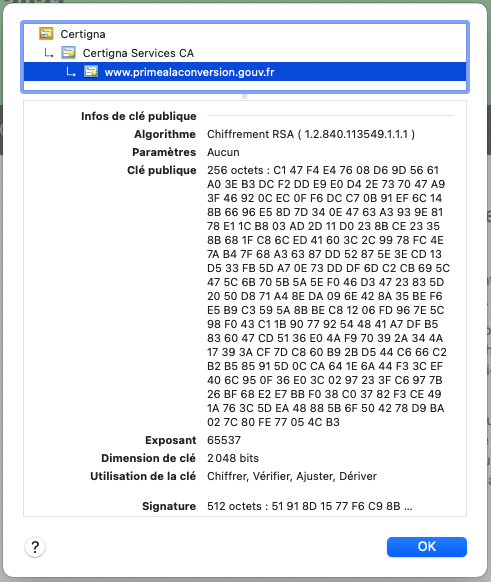
Dans le cas d’un site gouvernemental dont vous avez ci-dessus la clé publique en hexadécimal, en décimal ça donne :

2439947598582706702798526890529233120794876767819133149446658760869005736457282592987346080805916383 0284406586872704568580622174068987725809560368438846650255202189572054439527987416364066605586809793 6631418872707168138674999024729543292820113288254473386698081540810940403711849443572041577229866302 7341885788210068947325318209984820670582105216952621361991379685922155585417059924095010387002706390 4343947957035519478350754571894017523484945371960845293896409479030520095608110433980889979549676887 3498726813849226331678883464362866977662857407320685833981076308165253676075916784983839308766543963 37730841940937907

Un entier à 618 chiffres dont on sait qu’il est le produit de deux nombres premiers dont chacun s’écrit certainement avec plus de 300 chiffres. Est ce qu’il y en a tant que ça des nombres premiers ayant entre 300 et 400 chiffres ? la réponse est qu’il y en a beaucoup, beaucoup trop pour qu’on puisse trouver les diviseurs de la clé. En cherchant la répartition des nombres premiers vous tomberez fatalement sur la spirale d’Ulam qu’on va s’amuser à reproduire pour voir comment se répartissent les nombres premiers. Bien entendu on va rester sur des nombres à 6 chiffres et déjà c’est du lourd.

Ulam est un mathématicien polonais dont la légende raconte que l’ennui l’amena à écrire les entiers en décrivant une spirale autour de 1. Ensuite il entoura les nombres premiers pour s’apercevoir que ceux-ci s’alignaient. Si vous ne connaissiez pas du tout, je vous invite à lire l’histoire qui est très bien racontée ici : https://fr.wikipedia.org/wiki/Spirale_d%27Ulam.

Je me suis posé la question de savoir s’il était possible d’illustrer ça avec Excel et jusqu’où je pourrai aller sans pousser mon pc dans ses retranchements ? Plutôt que de remplir les cellules avec des chiffres – ce qui est fastidieux, il m’a paru plus judicieux de linéariser en plaçant les chiffres sur une grille du plan à 2 dimensions. Les points du plan dont les abscisses x et ordonnées y sont entiers seront les coordonnées d’un entier naturel déterminé comme suit :

-        à l’origine (x=0 et y=0) on place un nombre entier 0, 1, 41 ou ce qu’on veut

-        on incrémente l’entier en faisant un pas vers la gauche (x-1) et on obtient un deuxième point

-        on incrémente à nouveau en faisant un pas vers le bas (y-1) et c’est le troisième point

-        ensuite 2 pas vers la droite (x+1) (x+1) et 2 pas vers le haut (y+1) (y+1) en incrémentant à chaque pas

-        on fait de plus en plus de pas avant de changer de direction à mesure qu’on s’éloigne de l’origine car on prend soin de ne pas écraser les nombres déjà placés sur la grille.

Au final, les 16 premiers entiers se placent comme suit :

Chaque entier est repéré par une abscisse et une ordonnée, la spirale se dessine, ensuite on récupère les nombres premiers. On place les points sur le plan sans les relier et on a les 6 nombres premiers inférieur à 16 :

Maintenant qu’on a la méthode, il faut générer les entiers avec leurs coordonnées. Il y a ~41 000 nombres premiers entre 41 et 500 587 (en partant de 41 certains alignements sont plus flagrants). Donc reste à générer 500 546 lignes (Nombre ; PositionX ; PositionY) pour pouvoir positionner les nombres premiers dont on récupère les coordonnées en utilisant la fonction RECHERCHE d’Excel.

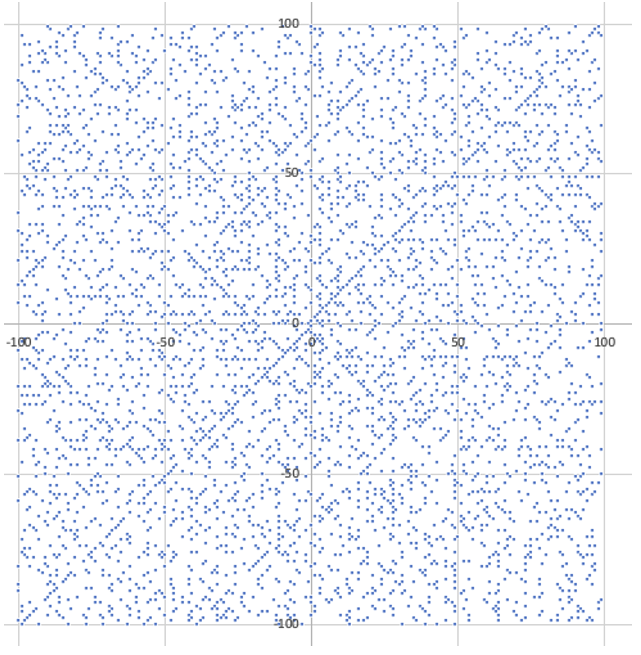
J’ai eu l’idée de générer les lignes en question avec une macro (écrit en VBA), très vite – c’est-à-dire qu’à partir de 5 000 points générés les temps d’exécution deviennent assez longs : jusqu’à plusieurs minutes. Je n’ose pas essayer d’aller jusqu’à 100 000 ni même 50 000. J’ai testé la génération de la spirale par python : ça se fait instantanément ; qu’à cela ne tienne, je génère les lignes par python sous forme de fichier CSV que j’intègre dans une feuille Excel, je recherche les nombres premiers sur la feuille et récupère les coordonnées à afficher dans un graphique sous forme d’un nuage de points. On commence avec les 4 189 nombres premiers entre 41 et 40 000 on voit que des lignes se dessinent et que la répartition n’est pas complètement aléatoire (fig. 1)

Figure 1

Et on continue avec les ~41000 nombres premiers < 501 000 fig. 2 générée avec Excel comme nuage de points c’était le l’objectif de départ.

Figure 2

Cette spirale a permis de trouver des équations quadratiques permettant de générer de grandes quantités de nombres premiers, mais on est loin de pouvoir trouver les nombres premiers « simplement ». Pour cela il faudrait démontrer l’hypothèse de Riemann[2] ou alors développer l’ordinateur quantique dont on nous dit qu’il effectuerait certains calculs plus rapidement qu’un ordinateur de la taille de l’univers observable[3]. Pour revenir à l’exemple de départ, sachant qu’il y a de l’ordre de n/log(n) nombres premiers plus petit que n, il y aurait de l’ordre de 10^297 nombres premiers à 300 chiffres – n étant de l’ordre de 10^300, log(n) serait plus petit que 1000 car log(10^300) est de l’ordre de 300. Si on était capable de tester un milliard de nombres par nanoseconde -ce qui est loin d’être la cas- il faudrait de l’ordre de 10^270 années pour les explorer. Donc on n’est pas en capacité de décomposer la clé publique à 618 chiffres en produit de deux nombres premiers.

Pour revenir à notre exercice de départ, on a réussi à visualiser la répartition des 41 000 nombres premiers plus petits que 500 000 dans une spirale dite d’Ulam. Excel est suffisamment puissant pour gérer un demi-million de points : les recherches et le graphique qui vont avec, mais il faut éviter de les générer par VBA, en tous cas je n’ai pas osé aller au-delà des 10 000 points. Il a fallu à VBA 27s pour 1 000 points, 152 s pour 5 000 et 341 s pour 10 000.

En python le temps d’exécution pour 500 000 points a été de 1.62 s… moins de temps qu’il n’en faut pour ouvrir le fichier.

Sachez jongler avec les différents langages selon les besoins que vous avez. Pour ce qui est d’Excel, il est devenu suffisamment puissant pour gérer des centaines de milliers de lignes pour peu que l’ordinateur sur lequel il tourne ait les « reins solides ».

On peut également visualiser les mêmes nombres premiers sur une spirale « classique » on y voit également que la répartition n’est pas aléatoire, mais pour le coup il n’y a nul besoin de programmation, une feuille Excel seule suffit à générer les points.

J'espère que vous avez trouver le sujet intéressant, n'hésitez pas à laisser un commentaire si vous souhaitez échanger sur le sujet.